저번 포스팅했던 RNN과 LSTM에 이어서 이번에는 Transformer에 대해 포스팅 해보도록 하겠습니다.
Transformer에 들어가기 앞서 Seq2Seq (Sequence to Sequence)와 Attention에 대해 알아보겠습니다.
Seq2Seq (Sequence to Sequence)

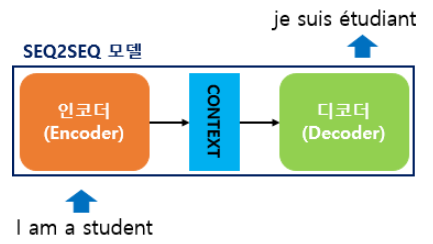
Sequence to Sequence는 번역기와 같이 Sequence Data가 Sequence Data로 나오게 되는 것이라고 보면 됩니다.
내부를 보면 Input Data를 받는 부분을 인코더 (Encoder)라 하고, Output 값이 나오는 부분을 디코더 (Decoder)라 합니다.

- 인코더 (Encoder)
- Context Vector: 모든 단어들을 순차적으로 입력받은 뒤, 모든 단어 정보들을 압축해서 하나의 벡터로 만듭니다.
- 디코더 (Decoder)
- Context Vector를 번역된 단어로 한 개씩 순차적으로 출력합니다.
- 인코더로부터 전달받은 컨텍스트 벡터는 디코더 RNN 셀의 첫번째 은닉 상태에 사용합니다.
- 디코더는 <sos>가 입력되면, 다음에 등장할 확률이 높은 단어를 예측합니다. 즉, 시작을 알리는 신호!
Attention
어텐션의 기본 아이디어는 디코더에서 출력 단어를 예측하는 매 시점(time step)마다,
인코더에서의 전체 입력 문장을 다시 한 번 참고한다는 점입니다.
단, 전체 입력 문장을 전부 다 동일한 비율로 참고하는 것이 아니라,
해당 시점에서 예측해야할 단어와 연관이 있는 입력 단어 부분을 좀 더 집중(attention)해서 보게 됩니다.

어텐션을 함수로 표현하면 주로 다음과 같이 표현됩니다.
Attention(Q, K, V) = Attention Value
어텐션 함수는
1. '쿼리(Query)'에 대해서 모든 '키(Key)'와의 유사도를 각각 구합니다.
2. 유사도를 키와 맵핑되어있는 각각의 '값(Value)'에 반영
3. '값(Value)'을 모두 더해서 리턴
여기서는 이를 어텐션 값(Attention Value)이라고 하겠습니다.
- Q = Query : t 시점의 디코더 셀에서의 은닉 상태
- K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
- V = Values : 모든 시점의 인코더 셀의 은닉 상태들
Dot Product Attention

Dot Product Attention은 Attention의 종류 중 하나로써 Attention의 이해를 돕기 위해 이를 기준으로 설명하겠습니다.
※ 사전 정의 ※
- 위 그림은 디코더의 세번째 LSTM 셀에서 출력 단어를 예측할 때, 어텐션 메커니즘을 사용하는 모습을 보여줍니다.
- 디코더의 첫번째, 두번째 LSTM 셀은 이미 어텐션 메커니즘을 통해 je와 suis를 예측하는 과정을 거쳤다고 가정
- 세번째 LSTM 셀은 출력 단어를 예측하기 위해서 인코더의 모든 입력 단어들의 정보를 다시 한번 참고하고자 합니다.
- 소프트맥스 함수를 통해 나온 결과값은 I, am, a, student 단어 각각이 출력 단어를 예측할 때 얼마나 도움이 되는지의 정도를 수치화한 값
- 인코더의 은닉 상태는 각각 \(h_{1}, h_{2}, h_{3}, h_{4}\) 입니다.
- 디코더의 은닉 상태는 현재 시점 기준 \(s_{t}\) 입니다.

시점 t에서 출력 단어를 예측하기 위해서 디코더의 셀은 세 개의 입력값이 필요합니다.
- 이전 시점 t-1의 은닉 상태
- 이전 시점 t-1에 나온 출력 단어
- 어텐션 값 (Attention Value) = \(a_{t}\)
※ Attention 값 구하기 ※
Attention 값을 구하기 위해서는 어텐션 스코어 (Attention Score)를 먼저 구해주어야 합니다.
어텐션 스코어란 현재 디코더의 시점 t에서 단어를 예측하기 위해,
인코더의 모든 은닉 상태 각각이 디코더의 현 시점의 은닉 상태 st와 얼마나 유사한지를 판단하는 스코어값입니다.
1. \(s_{t}\) 를 전치 (transpose) 하여 \(s_{t}^{T}\) 를 만들어 줍니다.

2. 각각의 \(h_{i}\) 와 내적을 시행해줍니다! - \(score(Q, K) = Q \cdot K\)
- \(score(s_{t}, h_{i}) = s_{t}^{T}h_{i} \)
3. \(s_{t}\) 와 \( h_{1}, h_{2}, ... \) 의 내적 모음을 \(e^{t}\) (어텐션 스코어 모음값) 이라고 정의 해줍니다.
- \(e^{t} = [s_{t}^{T}h_{1}, s_{t}^{T}h_{2}, ... s_{t}^{T}h_{i}]\)
- 각각의 값은 어텐션 가중치(Attention Weight)라고 합니다.

4. \(e^{t}\) 에 softmax를 적용하여 모든 값을 합하면 1이 되는 확률 분포를 얻어냅니다.
- \(a^{t} = softmax(e^{t})\)

5. 어텐션 값(Attention Value) 을 구해줍니다.
- \(a_{t}=\sum_{i = 1}^{N}a_{i}^th_{i}\)

6. 어텐션 값과 디코더의 t 시점의 은닉 상태를 Concatenate 합니다.
- \(a_{t}\) 와 \(s_{t}\)의 결합은 \(\upsilon_{t}\) 라고 합니다.
- \(\upsilon_{t}\) 를 \(\hat{y}\) 를 예측하는데 입력값으로 사용합니다.


7. 출력층 연산의 입력이 되는 \(\tilde{s}_{t}\) 를 구해줍니다.
- 논문에서는 \(\upsilon_{t}\) 를 바로 출력층의 연산에 보내기 전에 신경망 연산을 하나 추가해줬습니다.

8. \(\tilde{s}_{t}\) 를 출력층의 입력으로 사용하여 \(\hat{y}_{t}\) 를 구합니다.
이렇게 Key, Query, Value 개념에 맞게 Attention을 살펴 봤습니다.
이제 다음 게시물은 Transformer를 정리해서 올리겠습니다.
출처:
'Deep Learning > NLP' 카테고리의 다른 글
| 03. Transformer (0) | 2022.05.25 |
|---|---|
| 01. RNN, LSTM (0) | 2022.05.23 |